排序

# 912. 排序数组 (opens new window)

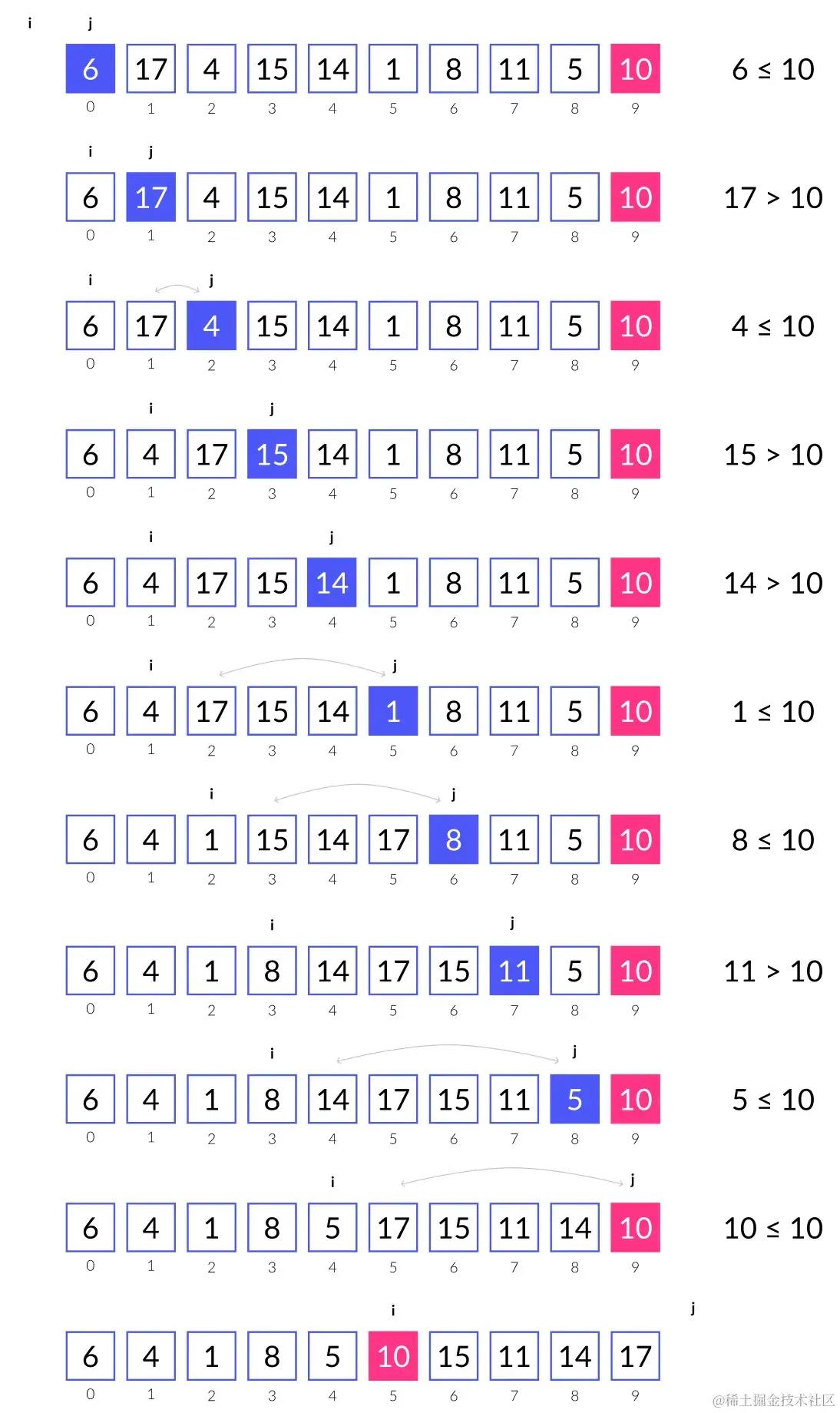
# 冒泡排序

class Solution {
    int[] nums;
    public int[] sortArray(int[] nums) {
        this.nums = nums;
        int n = nums.length;
        for(int j=n-1;j>0;j--){
            for(int i=0;i<j;i++){
                if(nums[i]>nums[i+1]){
                    swap(i,i+1);
                }
            }
        }
        return nums;
    }
    void swap(int l,int r){
        int tmp = nums[l];
        nums[l] = nums[r];
        nums[r] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 快速排序

时间复杂度：O(nlogn)~O(n^2)

当前区间内选择一个轴，区间中所有比轴小的数放到比轴的左边，大的放到轴右边；

最理想情况，选取的轴刚好在这个区间的中位数，就与归并排序一致；

最差情况，每次选取的轴刚好是最大值或最小值，每轮排序都需要进行n次比较，每次时间复杂度为O(n)，总时间复杂度为O(n^2)；

class Solution {
    int[] nums;
    public int[] sortArray(int[] nums) {
        this.nums = nums;
        if(nums==null || nums.length<2)
            return nums;
        shuffle();
        quickSort(0,nums.length-1);
        return nums;
    }
    void quickSort(int l,int r){
        if(l>r) return ;
        int p = partition(l,r);
        quickSort(l,p-1);
        quickSort(p+1,r);
    }
    int partition(int l,int r){
        int base = nums[r];
        int i = l;
        for(int j=l;j<r;j++){
            if(nums[j]<base){
                swap(i,j);
                i++;
            }
        }
        swap(i,r);
        return i;
    }
    void shuffle(){
        Random rand = new Random();
        int n = nums.length;
        for(int i=0;i<n;i++){
            int r = i+rand.nextInt(n-i);
            swap(i,r);
        }
    }
    void swap(int l,int r){
        int tmp = nums[l];
        nums[l] = nums[r];
        nums[r] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# 归并排序

时间复杂度：O(nlogn)，稳定

分治思想，每次将区间对半划分，直到长度为1；然后将相邻两个子区间进行合并;

每一层的时间复杂度为O(n)，共有logn层，总时间复杂度为O(nlogn)；

以最右边的数为轴：

class Solution {
    int[] nums;
    public int[] sortArray(int[] nums) {
        this.nums = nums;
        sort(0,nums.length-1);
        return nums;
    }
    void sort(int l,int r){
        if(l==r)
            return ;
        int mid = (l+r)>>>1;
        sort(l,mid);
        sort(mid+1,r);
        merge(l,mid,r);
    }
    void merge(int l,int mid,int r){
        int[] tmp = new int[r-l+1];
        int i=0;
        int p1=l,p2=mid+1;
        while(p1<=mid && p2<=r)
            tmp[i++] = nums[p1]<=nums[p2]?nums[p1++]:nums[p2++];
        while(p1<=mid)
            tmp[i++] = nums[p1++];
        while(p2<=r)
            tmp[i++] = nums[p2++];
        for(i=0;i<tmp.length;i++){
            nums[l+i] = tmp[i];
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 堆排序

提前知道数组，从最后一个元素下调heapify；（小数下调）

如果不知道所有数字，每个数字给出后上调heapInsert；(大树往上移)
void heapInsert(int[] arr, int index) {
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }
}
1
2
3
4
5
6

class Solution {
    public int[] sortArray(int[] nums) {
        if(nums==null || nums.length<2)
            return nums;
        // 每次heapify，第一个元素为最大元素；
        for(int i=nums.length-1;i>=0;i--)
            heapify(nums,i,nums.length);
        int heapSize = nums.length;
        swap(nums,0,--heapSize);// 最大的元素到了最后，就不是大根堆了
        // 重新调整大根堆，每次将最大元素移动至最后，堆大小-1
        while(heapSize>0){
            heapify(nums,0,heapSize);
            swap(nums,0,--heapSize);
        }
        return nums;
    }
    void heapify(int[] nums,int index,int heapSize){
        int l = index*2+1;
        while(l<heapSize){
            // 节点不一定有右子树，越界判断，将左右子树最大值下标给largest；
            int largest = l+1<heapSize && nums[l]<nums[l+1] ? l+1:l;
            // 若最大值大于父节点，进行交换，并继续向下传导，index=largest；
            if(nums[largest]<=nums[index])
                break;
            else{
                swap(nums,largest,index);
                index = largest;
                l = index*2+1;
            }
        }
    }
    void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 快速排序

# 75. 颜色分类 (opens new window)

参考：75. 颜色分类 - 力扣（LeetCode） (opens new window)

循环不变量写法一：

nums中：

[0,l) = 0 保证初始化为空，l=0，遍历到 0时先交换再加

[l,i] = 1

[r,n-1] = 2 保证初始化为空，r=n，遍历到 2时先减再交换

循环终止条件 i==r，循环可以继续条件：i<r；

如果首尾都是2，r一直左移到不是2的位置，再与i交换；

class Solution {
    public void sortColors(int[] nums) {
        int n = nums.length;
        if(n<2) return ;
        int l=0,r=n;
        int i=0;
        while(i<r){
            if(nums[i]==0){
                swap(nums,i,l);
                l++;
                i++;
            }else if(nums[i]==1){
                i++;
            }else{
                r--;
                swap(nums,i,r);
            }
        }
    }
    void swap(int[] nums,int l,int r){
        int tmp = nums[l];
        nums[l] = nums[r];
        nums[r] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

循环不变量写法二：

nums中：

[0,l] = 0 保证初始化为空，l=-1，遍历到 0时先加再交换

(l,i) = 1

(r,n-1] = 2 保证初始化为空，r=n-1，遍历到 2时先交换再减

循环终止条件 i==r+1，循环继续条件：i<=r

class Solution {
    public void sortColors(int[] nums) {
        int n = nums.length;
        if(n<2) return ;
        int l=-1,r=n-1;
        int i=0;
        while(i<=r){
            if(nums[i]==0){
                l++;
                swap(nums,i,l);
                i++;
            }else if(nums[i]==1){
                i++;
            }else{
                swap(nums,i,r);
                r--;
            }
        }
    }
    void swap(int[] nums,int l,int r){
        int tmp = nums[l];
        nums[l] = nums[r];
        nums[r] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 384. 打乱数组 (opens new window)

class Solution {
    int[] nums;
    int[] init;
    public Solution(int[] nums) {
        this.nums = nums;
        this.init = new int[nums.length];
        System.arraycopy(nums,0,init,0,nums.length);
    }
    
    public int[] reset() {
        System.arraycopy(init,0,nums,0,nums.length);
        return nums;
    }
    
    public int[] shuffle() {
        Random random = new Random();
        for(int i=0;i<nums.length;i++){
            int r = i+random.nextInt(nums.length-i);
            swap(i,r);
        }
        return nums;
    }
    void swap(int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 215. 数组中的第K个最大元素 (opens new window)

方法一：快排

class Solution {
    public int findKthLargest(int[] nums, int k) {
        shuffle(nums);
        int l=0,r=nums.length-1;
        k = nums.length-k;
        while(l<=r){
            int p = partition(nums,l,r);
            if(p<k) l = p+1;
            else if(p>k) r = p-1;
            else return nums[p];
        }
        return -1;
    }
    int partition(int[] nums,int l,int r){
        int base = nums[r];
        int i = l;
        for(int j=l;j<r;j++){
            if(nums[j]<base){
                swap(nums,i,j);
                i++;
            }
        }
        swap(nums,i,r);
        return i;
    }
    void shuffle(int[] nums){
        Random random = new Random();
        int n = nums.length;
        for(int i=0;i<n;i++){
            int r = i+random.nextInt(n-i);
            swap(nums,i,r);
        }
    }
    void swap(int[] nums,int l,int r){
        int tmp = nums[l];
        nums[l] = nums[r];
        nums[r] = tmp;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

方法二：优先级队列

class Solution {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        for(int num:nums){
            pq.offer(num);
            if(pq.size()>k){
                pq.poll();
            }
        }
        return pq.peek();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

# 归并排序

# 88. 合并两个有序数组 (opens new window)

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int[] arr1 = new int[m];
        for(int i=0;i<m;i++)
            arr1[i] = nums1[i];
        int[] arr2 = nums2;
        int i=0,j=0;
        int p = 0;
        while(i<m && j<n)
            nums1[p++] = arr1[i]>arr2[j]?arr2[j++]:arr1[i++];
        while(i<m)
            nums1[p++] = arr1[i++];
        while(j<n)
            nums1[p++] = arr2[j++];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 4. 寻找两个正序数组的中位数 (opens new window)

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length,n = nums2.length;
        int[] nums = new int[m+n];
        int i=0,j=0,k=0;
        while(i<m && j<n){
            nums[k++] = nums1[i]<=nums2[j]?nums1[i++]:nums2[j++];
        }
        while(i<m){
            nums[k++] = nums1[i++];
        }
        while(j<n){
            nums[k++] = nums2[j++];
        }
        if(k%2==0){
            return (nums[k/2-1]+nums[k/2])/2.0;
        }else{
            return nums[k/2];
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 327. 区间和的个数 (opens new window)

# 315. 计算右侧小于当前元素的个数 (opens new window)

class Solution {
    Pair[] tmp;
    int[] cnt;// 记录比自己小的个数
    public List<Integer> countSmaller(int[] nums) {
        int n = nums.length;
        this.cnt = new int[n];
        this.tmp = new Pair[n];
        Pair[] pair = new Pair[n];
        for(int i=0;i<n;i++){
            pair[i] = new Pair(nums[i],i);
        }
        sort(pair,0,n-1);
        List<Integer> ret = new ArrayList<>();
        for(int e:cnt){
            ret.add(e);
        }
        return ret;
    }
    void sort(Pair[] pair,int l,int r){
        if(l==r) return ;
        int mid = l+(r-l)/2;
        sort(pair,l,mid);
        sort(pair,mid+1,r);
        merge(pair,l,mid,r);
    }
    void merge(Pair[] pair,int l,int mid,int r){
        for(int i=l;i<=r;i++){
            tmp[i] = pair[i];
        }
        int i=l;
        int j=mid+1;
        for(int p=l;p<=r;p++){
            if(i==mid+1){
                pair[p] = tmp[j++];
            }else if(j==r+1){
                pair[p] = tmp[i++];
                cnt[pair[p].idx] += j-mid-1;
            }else if(tmp[i].val>tmp[j].val){
                pair[p] = tmp[j++];
            }else{   // 5,8(i)  6,10(j)
                pair[p] = tmp[i++];
                cnt[pair[p].idx] += j-mid-1;
            }
        }
    }
    class Pair{
        int val;
        int idx;
        Pair(int val,int idx){
            this.val = val;
            this.idx = idx;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

# 493. 翻转对 (opens new window)

# 169. 多数元素 (opens new window)

class Solution {
    public int majorityElement(int[] nums) {
        return rec(nums,0,nums.length-1);
    }
    // 返回众数
    int rec(int[] nums,int l,int r){
        // size为1的数组，该元素就是众数
        if(l==r)
            return nums[l];
        int mid = (l+r)>>>1;
        int leftHalf = rec(nums,l,mid);
        int rightHalf = rec(nums,mid+1,r);
        if(leftHalf == rightHalf)
            return leftHalf;
        int leftCount = countInRange(nums,leftHalf,l,r);
        int rightCount = countInRange(nums,rightHalf,l,r);
        return leftCount>rightCount?leftHalf:rightHalf;
    }
    int countInRange(int[] nums,int num,int l,int r){
        int cnt = 0;
        for(int i=l;i<=r;i++){
            if(nums[i]==num){
                cnt++;
            }
        }
        return cnt;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

← 差分数组滚动数组→